Chapter 5     Joint Distributions

5.1   Joint Densities & Independence

Goal:  Look at pairs of random variables (X, Y); result of experiment will give pair of values (one value for each)

ex:

Roll 2 dice; X = value on 1st die, Y = value on 2nd. Then the set of possible results of the experiment are the pairs of values
{ (1,1), (1,2), (1,3), ..., (1,6), (2,1), ....., (6,6) }

Note: we'll consider only the case where the random variables are discrete (not continuous)
 

Def:  Let X, Y be discrete r.v.’s. Then their joint probability density function is defined to be

f(x,y)  =   P( X = x  and  Y = y )
 
• f(x,y) gives the probability that the outcome of the experiment will be the pair of values (x,y)
• can represent the joint density function as a table

ex:

Plants are grown in a greenhouse; suppose the number of stems and number of blooms on each plant varies, with the number of stems being 1, 2, or 3 and the number of blooms being 0, 1, or 2.
Let X = # stems on a randomly selected plant: then possible values are x = 1, 2, 3
Let Y = # blooms on a randomly selected plant: then possible values are y = 0, 1, 2
Suppose that the joint density function of X and Y is given by the following table:

What’s the probability a randomly selected plant will have 2 stems and 1 bloom?

We want  P(X=2 and Y=1)   =   f(2,1)   =   .25

What’s the probability a randomly selected plant will have more stems than blooms?

We want   P(X > Y);   thus need to consider all the pairs (x,y) where x > y, i.e.,
P(X > Y)  =  P(X=1 and Y=0)  +  P(X=2 and Y=0)  +  P(X=2 and Y=1)  +  P(X=3 and Y=0)
+  P(X=3 and Y=1)  +  P(X=3 and Y=2)
=   f(1,0) + f(2,0) + f(2,1) + f(3,0) + f(3,1) + f(3,2)
=   .22 + .09 + .25 + .01 + .07 + .09
=   .73
What’s the probability a randomly selected plant will exactly 1 bloom?
We want   P(Y = 1);   thus need to consider all the pairs (x,y) where y = 1, i.e.,
P(Y = 1)   =   P(X=1 and Y=1) + P(X=2 and Y=1) + P(X=3 and Y=1)
=   f(1,1) + f(2,1) + f(3,1)   =   .12 + .25 + .07   =   .44
(Note that this just amounts to summing the entries in a particular column)
 
 
 

1. f(x,y)  >=  0    for all x, y
2. 

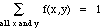
Can consider X or Y alone:

Def:  The marginal density for X is defined as

f_X(x)   =   P(X = x)
= 
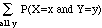
i.e.,


 

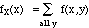
The marginal density for Y is similarly defined as

f_Y(y)   =   P(Y = y)
i.e.,

 

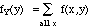
• thus the marginal densities are obtained by summing either the rows or the columns of the table for the joint density function
• called marginal densities because the natural place to write them is in the margins of the joint density table (see next example)

ex:

Consider the plant example above; find the marginal densities for X and Y
X:  f_X(x)  =  P(X = x), so
f_X(1)  =  P(X = 1)  =  P(X=1 and Y=0) + P(X=1 and Y=1) + P(X=1 and Y=2)
=   f(1,0) + f(1,1) + f(1,2)   =   .22 + .12 + 0   =   .34
f_X(2)  =   f(2,0) + f(2,1) + f(2,2)   =   .09 + .25 + .15   =   .49
f_X(3)  =   f(3,0) + f(3,1) + f(3,2)   =   .01 + .07 + .09   =   .17
Notice that we're just summing each row of the table!

Y:  f_Y(y)  =  P(Y = y), so

f_Y(0)  =  P(Y = 0)  =  P(X=1 and Y=0) + P(X=2 and Y=0) + P(X=3 and Y=0)
=   f(1,0) + f(2,0) + f(3,0)   =   .22 + .09 + .01   =   .32
f_Y(1)  =   f(1,1) + f(2,1) + f(3,1)   =   .12 + .25 + .07   =   .44
f_Y(2)  =   f(1,2) + f(2,2) + f(3,2)   =   0 + .15 + .09   =   .24
Just summing each column of the table!
 

These can be conveniently written right on the original table, in the margins!

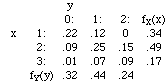
Independent Random Variables

Q:  do the values for X and Y depend on one another, i.e., does the value obtained for X influence in any way the value we get for Y? In other words, is the event  X = x  independent of the event  Y = y ?

Recall:
two events A, B were defined to be independent   iff

P(A  B)  =  P(A) P(B)

P(A  B)  =  P(A) P(B)

P(X=x and Y=y)   =   P(X=x) * P(Y=y)

f(x,y)  =  f_X(x) * f_Y(y)    for all values of x and y

We use the above condition as our definition:
 

Def:  discrete r.v.’s X and Y are  independent  iff the joint density is the product of the marginal densities, i.e., iff

f(x,y)  =  f_X(x) * f_Y(y)    for all values of x and y
 
• random variables X and Y are independent if the value obtained for X doesn't influence the value obtained for Y, and vice-versa

ex:

In the above plant example, the number of stems X and the number of blooms Y are not independent. This follows because the joint density isn't equal to the product of the marginal densities for all values of x and y. For example, for  x = 2 and y = 0,
f(2,0)  =  .09
but
f_X(2) * f_Y(1)  =  (.49) (.32)  =  .1568  =  .16  (to 2 decimal places)
 

ex:

Roll 2 dice;  let  X = value on first die, Y = value on second die. Then X and Y are clearly independent (the value on the first die can't influence the value that appears on the second), and we can use this to find the joint density function from the marginal densities using  f(x,y)  =  f_X(x) * f_Y(y).
Since  f_X(x) = 1/6  for x = 1, 2,..., 6   and   f_Y(y) = 1/6  for y = 1, 2,..., 6,
we get   f(x,y)  =  1/36   x, y  = 1, 2,..., 6.
But this is exactly what we'd expect: for example,  f(3,5) = probability that we get a 3 on the first die and a 5 on the second one, which equals 1/6 times 1/6! Thus we expect f(x,y) = 1/36 for all x, y.

ex:

Roll 2 dice;  let  X = value on first die, Y = sum of values on the two dice. Then X and Y are not independent; the value on the first die definitely influences the value that the sum can take on. To show that the definition isn't satisfied, we need to find a pair of values for x and y for which   f(x,y)  =  f_X(x) * f_Y(y)  doesn't hold.
Look at the case  x = 1  and   y = 12,  i.e., the case where the value on the first die is 1 and the sum of the values on the two dice is 12.

But this clearly can't ever happen: if the value on the first die is 1, the sum could be at most 7. Thus the value of the joint probability function is 0:

f(1,12)  =  0     ( P(X=1 and Y=12)  =  0 ).
 
Now look at the marginal density functions.
f_X(1) = 1/6;   the probability that we get a 1 on the first die (ignoring the value of the sum) is 1/6.
f_Y(12) = 1/36;   the probability that the sum of the two dice is 12 is 1/36, since the only way to get a 12 is to get a 6 on each die, giving 1/6*1/6 = 1/36 for the probability.
Thus
f_X(1) * f_Y(12)  =  1/6 * 1/36  =  1/216
 
But thus
f(1,12)  is not equal to  f_X(1) * f_Y(12),
so we've shown formally that X and Y aren't independent.