1.2 Sample spaces & Events
Def: Sample space: set of all possible outcomes of an
experiment; elements called sample points
-
usually denote by S
-
must include all possible outcomes
-
sometimes more than one possibility for S, depending on how outcomes are
specified
ex:
flip coin 3 times; sample space S is
S = {hhh, hht, hth, htt, thh, tht, tth, ttt} (8 possible
outcomes)
or
S = {3 heads, 2 heads & 1 tail, 1 head & 2 tails, 3 tails}
(4 possible outcomes)
either is acceptable as the sample space; which one is used might depend
on what we're interested in investigating. (The first has a very nice property
not shared by the second: each of the outcomes is equally likely to occur!
Because of this, we'll usually use the first as our sample space.)
ex:
Have 4 stages of a rocket; any one can fail, at which point mission
is over. A logical sample space representing all possible outcomes would
be
S = {f, sf, ssf, sssf, ssss},
where ssf represents the outcome in which the first two stages succeed
but the third fails. (Hopefully, outcomes not equally likely!!)
Def: An event is any subset of sample space (i.e., any set
of possible outcomes) - can consist of a single element
ex: (rocket)
The event that the rocket fails at some stage is subset A = {f, sf,
ssf, sssf}
The event that rocket goes through 2nd stage is subset B = {ssf, sssf,
ssss}
Notes:
-
The empty set
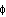 is a subset, hence an event; called the impossible event
is a subset, hence an event; called the impossible event
-
The entire sample space S is a subset, hence an event; called
the certain event
-
When the actual outcome of the experiment is a member of the subset, we
say the event has occurred
ex: (rocket)
if rocket blows up during 2nd stage; then event A above has occurred,
event B hasn't
Can consider union, intersection, complement of events to get new events
-
A
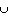 B:
either A occurs, or B occurs, or both
B:
either A occurs, or B occurs, or both
-
A
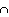 B: both A
& B occur
B: both A
& B occur
-
A': A does not occur
ex: (rocket)
A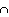 B = event rocket
fails and gets thru second stage = {ssf, sssf}
B = event rocket
fails and gets thru second stage = {ssf, sssf}
A' = event rocket doesn't fail = {ssss}
Def: Say events A & B are mutually exclusive if A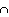 B
=
B
= 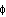
-
A and B have no outcomes in common
-
events A and B can't both occur simultaneously
ex: (rocket)
Let C = event rocket succeeds; then A & C are mutually exclusive.
A & B aren't; they share the outcomes ssf and sssf. In other words,
events A and B could both occur, if in the actual outcome the rocket fails,
but gets through the second stage.
Previous section Next
section