2.3 Independent Events
Def: Two events A, B are independent if and only if
P(A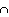 B) = P(A) P(B).
B) = P(A) P(B).
-
called the Multiplication Rule for Independent Events
-
makes it easy to compute P(A
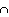 B)
if know just P(A), P(B)
B)
if know just P(A), P(B)
-
what does independence mean? Look at the conditional probability:
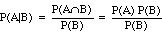 for A and B independent,
for A and B independent,
or P(A|B) = P(A).
-
the fact that B has occurred doesnít change the probability that A will
occur
-
knowledge that B has occured doesn't give us any additional information
as to whether or not A might also have occurred
-
A and B are independent if they "don't affect one another"
ex:
Flip a fair coin twice; use sample space S = {HH, HT, TH, TT}
to denote result of experiment. (A fair coin is one for which the probability
of getting a head or a tail on each flip is 1/2.) Compute the probability
of each outcome in the sample space.
Clearly, results of flips are independent; whether or not a head occurs
on the first flip has no bearing on whether or not a head will occur on
the second flip.
Let
H1 = event get head on 1st flip
H2 = event get head on 2nd flip
Then
P (two heads) = P(H1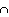 H2)
= P(H1) P(H2) since H1, H2 are independent
H2)
= P(H1) P(H2) since H1, H2 are independent
= (1/2) (1/2) = 1/4
Thus
The same reasoning follows for all other elements of the sample space;
thus
P(HT) = 1/4
P(TH) = 1/4
P(TT) = 1/4
Thus all of the elements of the sample space are equally likely.
ex:
Consider now a weighted coin, for which the probability of getting
a head is P(H) = .7 and the probability of getting a tail is
thus P(T) = .3. Flip this coin twice, and use sample space
S = {HH, HT, TH, TT} to denote possible outcomes. Compute the probability
of each outcome in the sample space.
As above, the results of the two flips are independent, so compute
as above using the multiplication rule for independent events:
P(HH) = P(H) P(H) = (.7) (.7) = .49,
P(HT) = P(H) P(T) = (.7) (.3) =
.21,
P(TH) = P(T) P(H) = (.3) (.7) =
.21,
P(TT) = P(T) P(T) = (.3) (.3) =
.09.
Notice that now the elements of the sample space are not equally
likely!
When it's not clear whether or not two events are independent, use
the definition (the multiplication rule) to see if they are, i.e., check
to see if P(A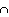 B)
= P(A) P(B).
B)
= P(A) P(B).
ex:
Let R = event it rains on a given day, and W = event itís windy. Suppose
P(R) = .30, P(W) = .20, P(R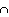 W)
= .15 ( = probability that it's both rainy and windy). Are these events
independent?
W)
= .15 ( = probability that it's both rainy and windy). Are these events
independent?
P(R) P(W) = .06, which is not equal to P(R 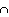 W).
W).
Thus the events are not independent, as we might expect: if it's rainy,
it's also likely to be windy.
General Multiplication Rule
If A, B independent, and know P(A) and P(B), easy to find P(A 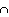 B) from the definition of independence:
B) from the definition of independence:
P(A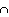 B) = P(A)
P(B).
B) = P(A)
P(B).
If A, B not independent, canít find P(A 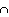 B) from just P(A) and P(B). But can always ue the definition of conditional
probability, as follows:
B) from just P(A) and P(B). But can always ue the definition of conditional
probability, as follows:
P(A|B) = 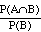
or
P(A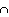 B) = P(B)
P(A|B)
B) = P(B)
P(A|B)
thus we take the probability that B will occur times the modified probability
for A, given that B has occurred!
ex: Urn model
Have 4 white balls, 2 black ones, in an urn. Draw 2 balls in
succession, without replacing 1st before drawing 2nd. Let the sample space
be {WW, WB, BW, BB}. Find the probability of each of the outcomes.
Note: can't use the multiplication rule for independent
events to find the results, i.e., can't use
P(WW) = P(W) P(W), since drawing a white ball on the first draw does
affect probability weíll get a white ball on the second draw (since there
will thus be fewer white balls in the urn) - these events aren't independent!
Let
W1 = event 1st ball drawn is white
W2 = event 2nd ball drawn is white
B1 = event 1st ball drawn is black
B2 = event the 2nd ball drawn is black
Since these events aren't independent, use the general multiplication rule:
P(WW) = P(W1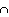 W2)
= P(W1) P(W2 | W1) = (4/6) (3/5) = 12/30
W2)
= P(W1) P(W2 | W1) = (4/6) (3/5) = 12/30
in this computation, P(W1) = 4/6, since initially there are 4 white
balls out of 6 total in the urn; but then P(W2|W1) = 3/5: the probability
of getting a white ball on the second draw, given that we got a white ball
on the first draw, is 3/5, since there are only 5 balls left in the urn,
of which 3 are white.
Similarly,
P(WB) = P(W1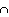 B2)
= P(W1) P(B2 | W1) = (4/6) (2/5) = 8/30
B2)
= P(W1) P(B2 | W1) = (4/6) (2/5) = 8/30
P(BW) = P(B1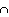 W2)
= P(B1) P(W2 | B1) = (2/6) (4/5) = 8/30
W2)
= P(B1) P(W2 | B1) = (2/6) (4/5) = 8/30
P(BB) = P(B1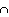 B2)
= P(B1) P(B2 | B1) = (2/6) (1/5) = 2/30
B2)
= P(B1) P(B2 | B1) = (2/6) (1/5) = 2/30
Previous section Next
section