2.2 Conditional Probability
Def: If A & B are events, then P(A|B) denotes the
conditional probability of A, given B.
and is defined as P(A|B) = 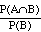 .
.
-
measures probability that A has occurred, given that we know B has
occurred.
-
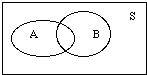
in Venn diagram, since we know B has occurred, we know we're in the region
for B, and we're essentially looking for the fraction of B's that are also
A's. This is given by the "area" of the overlap divided by the "area" of
B.
ex:
Selecting child at random; let H = event child has blonde hair, E =
event child has blue eyes
Suppose P(H) = .30, P(E) = .25, P(E H)
= .13
H)
= .13
What’s probability child has blue eyes, given that we know he has blond
hair?
We want
Note:
in general, the knowledge that event B has occurred will change the
value of the probability that event A has also occurred. In the above example,
knowing that a child has blond hair increases the chance that he/she has
blue eyes, as might be expected.
ex:
You’re dealt 2 cards from a standard deck of 52. What’s probability
that 2nd card is an ace, given that 1st card is ace?
Given that the first card selected is known to be an ace, there are
only 3 aces left in the 51 remaining cards, and thus the probability of
getting an ace as the second card is P = 3/51.
ex:
Extreme example: roll one die; let A = event number on
top is a 6, B = event number on bottom is a 1.
Then P(A|B) = 1! On a standard die, the numbers are arranged so that
the sum of the values on opposite faces equal 7 - thus the 3 is opposite
the 4, the 5 opposite the 2, and the 6 is opposite the 1. Thus if we know
that the 6 is on top, we know for certain that the 1 is on the bottom.
Previous section Next
section
![]() .
.