3.2 Discrete Probability Densities
Given a discrete random variable X; if x is one of its
possible values, want to know the probability that X takes
on the value x, i.e., want P(X=x).
Def: Let X be a discrete random variable. The function
f defined by
is called the probability density function (p.d.f.) of the
random variable X
Usually, the value of X depends on some underlying sample space S.
Find P(X = x) as follows:
-
determine the subset A of S on which X = x
-
then P(X=x) = P(A).
ex:
Flip 3 coins; sample space is S = {HHH, HHT, HTH, HTT,
THH, THT, TTH, TTT}
-
all outcomes equally likely (multiplication rule for independent events);
each has probability 1/8
Let random variable X equal the number of heads obtained; its
possible values are thus 0, 1, 2, 3
Then
P(X=0) = P({TTT}) = 1/8
P(X=1) = P({HHT, THT, TTH}) = 3/8
P(X=2) = . . .
= 3/8
P(X=3) = . . .
= 1/8
Thus the probability density function f is given in the
following table:
x f(x)
0 1/8
1 3/8
2 3/8
3 1/8
ex:
On AP Calculus exam, possible scores are 1, 2, 3, 4, 5. Let
Z = score of student chosen at random; then Z is a discrete
random variable. Suppose its p.d.f. is given by the following table:
ex:
Flip a fair coin until you get a tail; let N = total number of
flips.
sample space: { T, HT, HHT,
HHHT, HHHHT, ...}
probabilities : 1/2 1/4
1/8 1/16
1/32
value of N: 1
2 3
4
5
Thus probability of flipping n times before getting a tail is 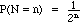 ,
,
and density function is
In tabular form:
Whatís the probability you'll flip less than 4 times before getting a tail?
P(N<4) = P(N=1) + P(N=2) + P(N=3)
= f(1) + f(2) + f(3) = 1/2 + 1/4 + 1/8 =
7/8.
Properties of probability density functions
Let f be the p.d.f. of random variable X. Then
-
f(x) >= 0 for all x
-
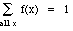 ,
where the sum is over all values that X can take on.
,
where the sum is over all values that X can take on.
These properties flow directly from the definition f(x)
= P(X = x): f(x) = the probability that X takes on the value
x. Thus the first property follows from the fact that all probabilities
must be positive, and the second from the fact that the sum of the probabilities
for all possible outcomes must be 1.
ex:
Consider r.v. N above, w/ p.d.f.
Note: the p.d.f. tells us everything we need to know about random
variable X; donít need to use the underlying sample space once we have
the p.d.f.
There is an alternate way to characterize random variables, closely
related to the probability density function:
Def: Given discrete random variable X. The function F defined
by
is called the cumulative distribution function of X. Thus F(x) gives
the probability that X will take on a value less than or equal to x.
The density function f and distribution function F are closely
related:
F(x0) = P(X <=
x0)
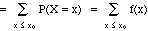
or
ex:
Consider the random variable N above, where N = the number of times
a coin is flipped before a tail appears. Find F(n) as both a table and
formula.
F(n) = P(N <= n),
so
F(1) = P(N<=1) = P(N=1) = f(1)
= 1/2
F(2) = P(N<=2) = P(N=1) + P(N=2) =
f(1) + f(2) = 1/2 + 1/4 = 3/4
F(3) = P(N<=3) = P(N=1) + P(N=2) + P(N=3)
= f(1) + f(2) + f(3) = 1/2 + 1/4 + 1/8 = 7/8
etc.
Thus it's clear that the value of F(n0)
is obtained by summing the values of f(n) for n <= n0.
The following table gives both f(n) and F(n):
From the table, a formula for F(n) can be inferred:
Previous section Next
section
,