3.3 Expectation, Mean & Variance
Def: The expected value or expectation
of discrete random variable X is denoted E(X) and is
defined as the weighted average of all possible values of X, with each
value weighted by the probability that value will occur:
i.e.,
.
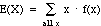E(X) is also called the mean of X, denoted m
ex:
On the Advanced Placement (AP) Calculus exam, possible scores are 1,
2, 3, 4, 5. Let Z = score of student chosen at random
be the discrete random variable with p.d.f. given by the following table:
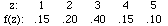
(Thus the probability that a student scores a 3 on the exam is
.40)
What's the expected value of Z?
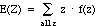
= 1·f(1)
+ 2·f(2) + 3·f(3) + 4·f(4) + 5·f(5)
= 1·(.15)
+ 2·(.20) + 3·(.40) + 4·(.15) + 5·(.10)
= 2.85
What does this mean? How can this be the expected or average score,
when a student can't ever get a score of 2.85 (the scores must be whole
values)?
The expected value gives the value that would result if we sampled a
large number of students, and found the average of their scores on the
test.
ex:
Consider a lottery like the Pennsylvania Daily Number, in which a 3-digit
number is chosen at random. Suppose it costs $1 to play, and if you pick
the correct 3-digit number, you win $500. (This is simpler than the real
lottery, which has has more different ways in which you can win.)
Let W represent your net winnings in one play of the lottery;
then W is a discrete random variable, which takes on the values
-1 and 499 (if you don't win, you lose the $1 it cost to play; if you do
win, you get $500 back, but you're out the dollar it cost to play).
The probability of winning is 1 out of 1000, or .001 : there are
1000 possible 3-digit numbers, out of which yours is one.
The probability density function for W is thus given in
the following table:
What is the expected value of W?
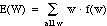
= (-1)·f(-1)
+ (499)·f(499)
= (-1)·(.999)
+ (499)·(.001)
= -.50
What does this mean? This is the long-term average winnings per trial:
if you play many times, you should expect to lose on average .50 each time
you play - if you play 1000 times, you should expect to be down $500, if
you play 4000 times, you should expect to be down $2000, etc.
If random variable Y is a function of random variable X, Y = H(X), the
expected value of Y is defined to be
-
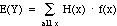
Most important functions are powers X2,
X3, ...
-
The expected values of these are called the moments of X:
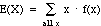= first moment
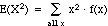= second moment
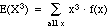= third moment
etc.
ex:
In the AP example above, compute the second & third moments of
Z.
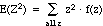
= 12·f(1)
+ 22·f(2) + 32·f(3)
+ 42·f(4) + 52·f(5)
= 12·(.15)
+ 22·(.20) + 32·(.40)
+ 42·(.15) + 52·(.10)
= 9.45
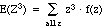
= 13·f(1)
+ 23·f(2) + 33·f(3)
+ 43·f(4) + 53·f(5)
= 13·(.15)
+ 23·(.20) + 33·(.40)
+ 43·(.15) + 53·(.10)
= 34.65
ex:
Consider the random variable N above, where N = the number of times
a coin is flipped before a tail appears. Compute the mean and second moment.
mean m = E(N) =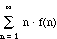 
= 1·(1/2) + 2·(1/4) + 3·(1/8) + 4·(1/16)
+ ....
glitch: infinite sum! While techniques exist to find the value of this,
it's still difficult. The second moment is even worse! Luckily, we'll look
at another technique for finding the moments e next section (using the
moment generating function). We'll revisit this computation then!
Note: If we know all of moments, can reconstruct the density
function of X other words, the moments completely determine the random
variable.
Rules for Expectation
Given random variables X, Y, constant C. then
-
E(c) = c
-
E(cX) = cE(X)
-
E(X + Y) = E(X) + E(Y)
Note: E(XY) * E(X) · E(Y), in general!
ex:
AP scores; pick 200 students at random; scores are Z1, Z2,
Z3, ..., Z200. Look at
the average of the 200 scores, i.e., let
What's the expected value of Y?
E(Y) =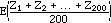 
= 
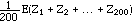by rule 2
= 
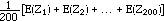by rule 3
= 
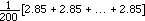
= 2.85
Thus the expected value for the average of a set of scores is the same
as the expected value of a single score! Note that the number of scores
used (200 here) is immaterial; the same conclusion would result. This will
be an important result when we look at sampling and statitics.
Def: The variance of random variable X is
defined as
The standard deviation (s.d.), s, is
s =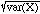 
-
the variance calculates the expected value of the squared deviation of
X from its mean m
-
the variance and s.d. measures the variability of the values X takes on;
the larger the variance or s.d., the more likely the values will vary widely
from the mean.
-
most of time, values X takes on will lie with in 1 side of the mean!
Simplified formula for computing var(X):
var(X) = E(X2) - m2
(or var(X) = E(X2) - E(X)2 )
folows from rules for expectation:
var(X) = E((X-m)2)
= E (X2 - 2Xm + m2)
= E (X2) - 2m E(X) + E(m2)
= E (X2) - 2m·m
+ m2 (note
that E(X) = m)
ex:
AP example; compute the variance and standard deviation.
var(Z) = E(Z2) - m2
;
but computed above that E(Z2) =
9.45 and E(Z) ( = m)
= 2.85,
so gives var(Z) = 9.45 - (2.85)2
= 1.3275,
and thus s =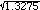 
= 1.15
What does this tell us? The standard deviation ls us the range into
which our scores will fall most of the time: most of the time the scores
will be within 1.15 units of the mean (2.85).
Rules for variances
Given random variables X, Y, constant c.
-
var(c) = 0
-
var(cX) = c2 var(X)
-
If X & Y are independent random variables, var(X + Y) = var(X)
+ var(Y)
Note: X, Y are independent if the value obtained for X doesn’t
influence the value obtained for Y,i.e., the value of Y doesn't depend
on the value of X; more on this later!
ex:
independent vs. dependent random variables
-
Roll 2 dice; X = value on 1st, Y = value on 2nd.
Then X and Y are clearly independent: the value on the first die doesn't
affect in any way the value that will appear on the other.
-
Roll 1 die; X = value on top, Y = value on bottom.
Then X and Y are clearly dependent: the value on the bottom is completely
determined by the value on the top.
-
Roll 2 dice; X = value on 1st, Y = sum of values on the two dice.
The X and Y are dependent: the value of Y, the sum, is not completely
independent of the value on the first die. For example, if the value on
the first die is a 6, then the sum can't take on any value less than 7.
Previous section Next
section
