Chapter 7 Estimation
-
want to estimate a parameter of a population (mean, say) using some statistic
computed from a sample (sample mean, say)
-
want the estimators to be good in the sense that
for most sample, want the value given by the estimator to be close
to the true value of the parameter it’s estimating.
7.1 Unbiased Estimators and Variability
Def: Let p be the value of some population
parameter, and let statistic 
be an estimator for p computed from a random sample. (Note
that
is a random variable: its value depends on the particular sample selected.)
Then
is said to be an unbiased estimator of p if
E()
= p
i.e., the expected value of the estimator is the value of the population
parameter.
-
this is a desirable property for an estimator to posess; it indicates that
the values given by the estimator from sample to sample will tend to be
centered around the true value of the population parameter, rather than
being consistently too high or too low
In addition to having the values given by an estimator being centered around
the true value of the population parameter it's estimating, we'd also like
the values to have a narrow spread, i.e., we'd like them on average not
to vary too far on either side of the expected value. To measure this,
we'll look at the standard deviation (variance) of the estimator; this
will tell us how far on average the values of the estimator will vary from
the expected value.
The most important estimators are
-
the sample mean
estimating the population mean m
-
the sample variance S2 estimating the population variance s2
Consider the expected value and standard deviation (variance) of these
two estimators.
Sample mean
1. Expected value (unbiasedness)
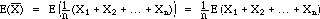(The above steps follow from properties of expectation, and from the fact
that since each of the random variables Xi in the sample comes
from the population being considered, the expected value of each is m)
-
Thus the expected value of
is m, i.e., the observed values for
over many samples would be centered at the true population mean m.
-
Note that this doesn't depend on the type of distribution of the population!
2. Variance (variability)
Look at the variance of
to see how widely the values of
can be expected to vary from sample to sample.
-
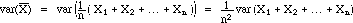
Thus the variance of the sample mean is the variance of the population
divided by n, the sample size; the values of the sample mean from sample
to sample will tend vary less than the values of single individuals selected
from the population
-
The larger the sample size, the smaller the variance of ,
and thus the less the observed values of
will tend to vary from the value of m. Thus
larger samples will tend to give more accurate estimates than smaller samples.
-
Note that again these results don't depend on the type of distribution
of the population
In fact: as n approaches infinity, the variance of
will approach 0, and thus the probability that the value given by
will differ from m goes to zero! This is known
as the Law of Large Numbers.
Sample Variance
1. Expected value (unbiasedness)
It can be shown that the expected value of S2 is s2,
i.e., that E(S2) = s2.
See the text for the derivation; the derivation is a little gory algebraically,
but uses properties of expectation as in the above derivations. However,
it's worth noting that it becomes clear in the derivation that we must
have n - 1 in the denominator of the expression for S2 in order
for it to be unbiased.
2. Variance (variability)
Alas! The expression for the variance of S2 depends
on the type of distribution of the population! However, under some
general assupltions, it can be shown that the variance of S2
decreases as the size of the sample increases, as was the case for the
sample mean. Thus the larger the sample, the more accurate the value given
by the sample variance.
-
we’ll consider the special case when the population has a normal distribution
later!
Previous section Next
section
