6.3 Sample Statistics
Def: A statistic is a function of the random
variables X1, X2, ..., Xn
of a random sample
-
used to estimate the values of population parameters
-
since itís a function of random variables, itís a random variable itself
The most important statistics are:
Def: The sample mean  is defined as
is defined as
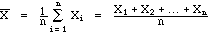
-
 is a random variable;
its value will vary from sample to sample
is a random variable;
its value will vary from sample to sample
-
its value for a given sample is just the usual average of the observed
values of X1, X2, ..., Xn
-
used to estimate the population mean
ex:
Heights of students; suppose a random sample of 25 students is selected
from the student population at large, and their heights are recorded, giving
following values:
70, 68, 65, 69, 77, 62, 70, 70, 61, 72, 64, 62, 69, 72, 73, 69, 63,
72, 69, 71, 70, 64, 68, 75, 61
Then the value of the sample mean for this sample is
Note: this value will be computed by SPSS or any other statistics software
package
Def: The sample median 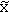 of a random sample is defined as follows:
of a random sample is defined as follows:
-
the observed values from the sample are put in increasing order
-
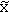 is the middle value
if n is odd, or halfway between the two middle values if n is even
is the middle value
if n is odd, or halfway between the two middle values if n is even
ex:
For the student heights above, if the values are put in increasing
order, we get
61, 61, 62, 62, 63, 64, 64, 65, 68, 68, 69, 69, 69, 69, 70, 70, 70,
70, 71, 72, 72, 72, 73, 75, 77
The sample median is given by the middle value, which is 69, so 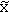 = 69.
= 69.
Def: The sample variance S2 is defined as
-
this is the average of the squared deviations of the sample values from
the sample mean
-
used to estimate the population variance s2
-
the sample standard deviation, S, is the square root of the sample variance
Q: Why use n-1 instead of n in formula?
A: S2 is a random variable used
to estimate the value of the population variance s2
. Though its value will vary from sample to sample, being sometimes a little
greater than s2 and sometimes a little
less, we would like its value to be a good estimate to the value of the
population variance for most samples. In particular, we wouldn't want it
to give high values more often than it gives low values, or vice versa.
As such, we would like the expected value of S2 to be s2,
i.e., the average value of the sample variances from a large number of
samples should be the population variance. Weíll see that the n-1 is needed
for this to be true; if we used n in the quotient, the values of the sample
variance would tend to consistently underestimate the value of the population
variance.
ex:
For the student heights above, the sample variance and standard deviation
are
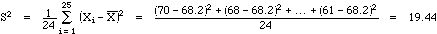
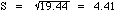
Previous section Next
section
is defined as
of a random sample is defined as follows: