7.4 Confidence Intervals
Idea: Use the value of 
from a sample to try to find an interval in which the true population mean
m is likely to lie
Consider: Suppose original population is normal, with mean
m, standard deviation s
-
from the results in the previous section,
is normally distributed, with
mean m, standard deviation
s/.GIF)
.
-
since is normally
distributed, can use the normal probability rule:
or
P( | - m
| < 2 s/
) = .95
since m
= m and s
= s/
i.e.,
95% of samples will have
lying within 2 s/
of the population mean m,
or equivalently,
for 95% of samples, m will lie within 2
s/
units of the sample mean
or
Gives an interval for m such that for 95% of
samples, m will lie in the interval!
Called a 95% confidence interval
Actually, slightly more than 95% of values lie within 2 standard deviations
of the mean; to get exactly 95%, we need to use those values that are within
1.96 standard deviations of the mean. Thus a slightly refined 95% confidence
interval is
Glitch: to use this, need to know s
for popluation!
ex:
Have a machine filling bags of popcorn; weight of bags known to be
normally distributed, and machine is such that mean weight m
is adjustible, but s.d. s is a built-in tolerance
for machine: s = .3 oz.
Take sample of 40 bags; average weight for the sample is
= 14.1 oz.
What’s a 95% confidence interval for mean m?
From the above, we know that for 95% of samples,
or
or
Thus assuming ours is one of the 95% of "good" samples, the true value
of the population mean m will lie in the interval
Why are we 95% confident? Because we could have gotten a bad sample!
In fact, only for 95% of the samples we could choose will the value of
the population mean m lie in the specified interval;
for 1 in 20 samples, the "bad" or nonrepresentative samples, the true mean
will lie outside of specified interval, and we'll draw an incorrect conclusion
by assuming it is in the specified range!
99% Confidence Interval
Goal: find an interval such that for
99% of samples, the true value of m will lie
in the specified range!
Approach:
-
is normally distributed,
with mean m
= m and standard deviation s
= s/
-
thus
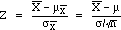is a standard normal random variable
-
let z.005 be the value such that
P( Z >= z.005) = .005, i.e., the area
under the density curve for Z to the right of z.005
is .005; z.005 is called the upper .005 critical value
-
Then
P(-z.005 <= Z <= z.005)
= .99 (i.e., the probability that Z will lie between
+z.005 and -z.005 is .99)
so
i.e., for 99% of samples the value of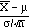 
will lie in the range
-
Solving the inequality for m, we get that
for 99% of samples, m will lie in the range
This is our 99% confidence interval for m
The .005 critical value can be found from (accurate) tables, and has
the value z.005 = 2.576
This gives the interval
ex:
Cereal boxes: using the data from the example above, we can construct
a 99% confidence interval for the mean m:
or
or
or
Note:
-
can never be 100% confident that the true value of the population mean
lies in the specified interval!
-
the higher the confidence level, the wider the interval must be!
Using the above argument, we can derive confidence intervals for any desired
level of confidence; we'd get
A (100 - a)% confidence interval for m
(given that s is known) is given by
where za/2 = upper a/2
critical value. (Note that the probability associated with the critical
value is half that of the "uncertainty" associated with the confidence
interval - we use za/2 for the (100
- a)% confidence interval. For example, for
the 95% confidence interval (where we are going to draw the wrong conclusion
5% of the time, i.e., the probability of making a mistake is .05), the
critical value used is z.025 !
Usual confidence levels and associated critical values:
90%: z.05 = 1.645
95%: z.025 = 1.960
99%: z.005 = 2.576
ex:
The 90% confidence interval for m for the
cereal example would be
Sample size vs. Accuracy
A 100% - a% confidence interval for m
is
-
the width of the interval is
-
the larger the sample size n, the narrower the interval!
-
often, choose sample size to give desired accuracy at a specified confidence
level.
ex:
Thus we,d need a sample size of almost 3500 boxes of cereal for the
95% confidence interval to give us an accuracy of .01 ounce.
Previous section Next
section
