3.5 The Binomial Distribution
Def: A random variable X is a binomial random variable if
it arises as the result of the following type of process:
-
have a fixed number n of Bernoulli trials (success (s) or failure (f) for
each)
-
the trials are independent, probability of success on each trial is same
(as before, denote probability of success as p, probability
of failure as q)
-
X = total number of successes in the n trials. (possible values
are 0 to n)
(in short, X is binomial if it "counts the number of successes in n trials.")
ex:
Test with 3 questions; have probability of .8 getting any of questions
correct. Let X = the number of questions you get correct. Then
X is a binomial random variable, with n = 3 (3 trials) and
p = .8 (probability of success on each trial), since it counts the
total number of successes in a fixed number of trials. A sample space giving
the 8 possible outcomes of your exam is shown below; beneath each outcome
is the corresponding value of X; beneath this is the probability of that
particular outcome (as before, these are found using the multiplication
rule for independent events).
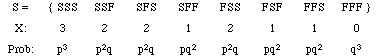
From the above we can get the probability density function, given in
the following table:
The density for a binomial random variable X with parameters n and p is
f(x) = 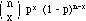 , x = 0, 1, 2, ..., n
, x = 0, 1, 2, ..., n
Its moment generating function is
(see text for the derivation).
From this, we can compute the first and second moments, and use these
to compute the mean and variance:
E(X) = 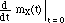 =
= 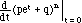
= n (pet + q)n-1 (pet) |t=0
(by the chain rule)
= n (p + q)n-1 (p) = np
(since p + q = 1)
E(X2) = 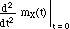 =
= 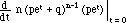
= n (n-1) p2 + np (when the
smoke clears, using the product and chain rules to differentiate; do this
as an exercise!)
These give us
var(X) = E(X2) - E(X)2 =
np(1-p) (exercise)
Thus the mean and variance are
m = np
var(X) = npq = np(1-p)
(so the standard deviation s
= 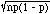 )
)
ex:
Suppose you take a test like the one above, in which the probability
of your getting any one of the questions correct is .8, but suppose now
the test has 20 questions. What’s the expected number of questions
you'll get correct?
Let X = the number of questions out of the 20 you get correct;
then X is a binomial random variable, with n = 20 and p = .8. Then
E(X) = np = (20)(.8) = 16, i.e.,
you'd expect to get 16 of the 20 correct.
What’s the probability you'll get exactly 1 wrong (i.e., 19 correct)?
P(X = 19) = f(19) = 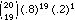 = .058
= .058
What's the probability you'll get 14 or fewer correct?
We want P(X <= 14) = F(14)
there's no convenient formula for F(x) for a binomial random variable.
We could compute F(14) by summing f(1) + f(2) + ... + f(14), but this is
tedious. Fortunately, values of F(x) for binomial random variables have
been tabulated for various values of n and p; your text has tables in the
back (p. 720-724) giving values for n = 1 through 20 and p = .1 through
.9. Using the table on p. 724 for n = 20 and p = .8, we find
P(X <= 14) = F(14) = .1958;
thus there's only about a 20% chance you'd get 14 or fewer correct.
Note: Though the tables only go up to n = 20, we'll find
there's a quick way for us to approximate the value of probabilities for
larger values of n using the normal distribution (to be discussed shortly).
ex:
A binary packet consisting of 64 bits is sent over a communications
line. Because of noise, some of the bits will be corrupted when they
are sent (i.e., they'll be sent as 1's or 0's, but will be received as
the opposite). Suppose the the probability that any 1 bit is corrupted
during transmission is p = 02.
What’s the expected # of bad bits in a packet?
Let X = # of corrupted bits received out of the 64 sent. Then
X is a binomial random variable, with n = 64 and p = .02 (here, "success"
is interpretted as a bit being corrupted). Thus
E(X) = np = 64*(.02) = 1.28
On average, we would expect 1.28 bits to be corrupted per packet.
What’s the probability the message comes through correctly (i.e., #
bad bits = 0)?
P(X=0) = 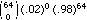 = .27
= .27
So only about 1/4 of the 64-bit packets sent would be expected to come
through without any errors.
In this situation, since most of the pakets will be corrupted, but usually
only by about 1 bit, it would make sense to use an error-correcting code
to transmit the data which can correct for errors in 1 or 2 bits.
Previous section Next
section