Chapter 4 Continuous Distributions
4.1 Continuous Random Variables and Densities
Recall: X is a continuous random variable if the possible values
for X form a continuous range or interval.
ex: Let L = length of leaf picked from tree; could
take on any value in interval [0, 10]
Important note:
-
It doesn’t make much sense to ask “what’s probability L = 2.5 inches”
. The chance that L = exactly 2.500000000000...
inches should be 0.
-
For a continuous random variable, the probability that X takes on any one
specific value is zero:
P(X=x) = 0
for any x.
Instead, we'll ask for the probability that the value of X will lie in
some range of values, usually an interval: want to know the probability
that the value of X lies between two specified values a and b, P(a
<= X <= b).
Can characterise continuous random variables with density function f(x);
however, it will have a very different meaning from its interpretation
in the discrete case!
Def:
Let X be a continous random variable. Then the density function
f of X is the function for which
i.e., the probability that X lies between a & b is the area under
the graph of f (x) from a to b.
The density function for a continuous random variable must satisfy 2
properties:
-
f(x) >= 0 for all x
this says the height of the graph must be >= 0 for all x
-
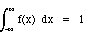
this says the probability that X lies between -•
and • must equal 1: X has to take on some
value!
Note: The probability of X taking on one specific value
should be 0. Indeed, by the above definition of the density function,
P(X=a) = P(a <= X <= a) =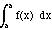 
= 0.
ex:
Let X = weight of cereal in a randomly selected box; suppose density
function of X is
The graph of f is:
What’s probability X lies between 14.5 and 15.5 ounces?
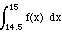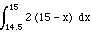
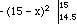P(14.5 <= X <= 15) = 
= 
= 
= 0 - (- (.5)2) =
.25
What’s probability X <= 14.2?
P(X <= 14.2) = P(-•
< X <= 14.2) =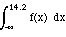 
= 
= 
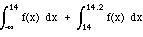
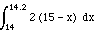(since f(x) = 0 for x <= 14)
= 
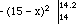= .36
What’s probability X >= 16?
P(X >= 16) = P(16 <= X < •)
= 
= 0; since f(x) = 0 for x > 15, the area under
the curve from x = 16 to x = •
is 0.
Can characterize a continuous random variable by its cumulative distribution
fn:
Def: The cumulative distribution function F of a
continuous random variable X is defined to be
-
notice that this is the same definition used in the discrete case.
-
also called the cumulative probability function
If the density function of X is f(x), then
,
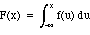since P(X <= x) equals the area under the graph of f
to the left of x.
ex:
For the example involving the weight of cereal boxes above, the cumulative
distribution function is found as follows:
for x <= 14, F(x) = 0; this follows because
P(X <= x) = 0 for any x less than 14, since the density function f(x)
= 0 to the left of 14 and hence the area under the curve to the left of
x is 0.
for x >= 15, F(x) = 1; this follows because
P(X <= x) = 1 for any x greater than 15, since the entire "hump"
of the density function will lie to the left of x and hence the area under
the curve to the left of x will be 1.
for x between 14 and 16, we have
F(x) = P(-• <=
X <= x) =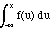 
= 
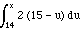(since f(x) = 0 for x less than 14)
= 
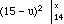= 1 - (15 - x)2
Thus we have
The graph of F is:
The distribution function in the example above illustrates certain features
shared by all cumulative distribution functions:
Properties of cumulative distribution functions
-
0 <= F(x) <= 1 for all x
-
-
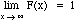
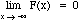
Note: F(x) will be continuous!
Previous section Next
section
