4.5    Normal Probability Rule & Chebyshev’s Inequality

Let X be a normal random variable, with mean  m,  standard deviation  s.
Then
• The probability that X lies within 1 s.d. of the mean is .68
• The probability that X lies within 2 s.d. of the mean is .95
• The probability that X lies within 3 s.d. of the mean is .997

• Useful for “quick & dirty” estimates
• Can be used only with normal random variables
• Follows from the fact that:

the probability that X lies within 1 s.d. of the mean
=  P(m - s  <=  X  <=  m + s);
using the standard normal random variable to compute this,
let  Z =  ;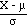
when  X = m - s,  Z  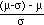=   =  -1
when  X = m + s,  Z  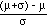=   =  1
so
P(m - s  <=  X  <=  m + s)  =  P(-1 <= Z <= 1)  =  .68   using the table for Z.
The other two parts follow in the same way.
 
 

Consider IQ scores; as discussed in the previous section, these are normally distributed with mean 100, s.d. 15. Then the Normal Probability Rule gives the following information:
• 68% of people have IQ scores within 1 standard deviation of the mean, i.e., between 85 and 115
• 95% of people have IQ scores within 2 standard deviations of the mean, i.e., between 70 and 130
• 99.7% of people have IQ scores within 3 standard deviations of the mean, i.e., between 55 and 145

Chebyshev's Inequality

Chebyshev’s inequality gives similar estimates which are applicable to any random variable (not just normal distributions)
 

Theorem Chebyshev’s Inequality
Let X be a random variable w/ mean m, standard deviation s.
Then

P(|X - m| < k s)  >=  1 - 1/k²,

Specific values of k give specific information:

• k=1:  the probability that X lies within 1 s.d. of the mean is at least  1 - 1/1² = 0.

gives no info!
• k=2:  the probability that X lies within 2 s.d. of the mean is at least  1 - 1/2²  = .75

thus for any distribution, at least 75% of the values will lie within 2 standard deviations of the mean
• k=3:  the probability that X lies within 3 s.d. of the mean is at least  1 - 1/3²  = .89

for any distribution, at least 89% of the values will lie within 3 standard deviations of the mean

Notes:

• these results are consistent with results for normal random variables; just gives less precise info!
• often useful for estimates when don’t know the exact distribution, and suspect normal distribution is not appropriate!
• graphically, these say that the area under the density curve from  x  =  m - 2s  to  x  =  m + 2s  is at least .75

Suppose that the length of 20 years worth of baseball games has been investigated, and that it has been found that the average (mean) length of a game is 165 minutes and the standard deviation is 32 minutes. Since we don't know whether or not the distribution of game times is normal, we can't use the normal probability rule to get information about how likely it is that a game will last a particular length of time; however, we can use Chebyshev's Rule:
• the probability that a randomly selected game will have a length within 2 standard deviations of the mean is at least  .75,  i.e., at least 75% of games will last between  165 - 2(32)  =  101 minutes  and  165 + 2(32)  =  129 minutes.
• the probability that a randomly selected game will have a length within 3 standard deviations of the mean is at least  .89,  i.e., at least 89% of games will last between  165 - 3(32)  =  69 minutes  and  165 + 3(32)  =  261 minutes.
This information might be useful if we had to estimate the number of hours that security personnel would be on duty: about 90% of the time we'd expect to have to pay them for between about 1 and 4 hours of work.