4.6   Normal Approximation to the Binomial Distribution

Binomial distribution:

• distribution of random variable X which counts # of successes in n independent trials with probability of success p on each trial.  (“coin flips”)
• X is a discrete random variable
• density function:   f(x)  =  
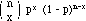
• mean:   m  =  np
• variance:   var(X)  =  np(1 - p)

Recall that in the discrete case, density function gives probability that particular outcomes will occur:
f(x)  =  P(X = x). Can present density function as a table of values.

ex:  binomial distribution with   n=5,  p=.30;  then density function f(x) given in table below:

Then:

• probability that particular value x will occur = height of bar over this value:

    P(X = x) =height of bar.
• with widths of bars equal to 1, area of each bar = height * width = height; thus

    P(X = x)  =  area of bar.
• Thus can use areas to find probabilities, as with continuous random variables;
P(X = x)  =  P(x - .5  <=  X  <=  x + .5)  =  area of bar between x - .5 and x + .5
 
In example above, to compute P(2 <= X <= 3), could approach as follows
P(2 <= X <= 3)   =   P(1.5 <= X <= 3.5)
=   sum of areas of bars lying between x = 1.5 and x = 3.5
=   .309 + .132  =  .441
Of course, gives same result we'd get just by using density function table.
• When n is large, tops of rectangles seem to form a smooth curve; if we knew what this was, we could use it to find areas & hence probabilities with integrals (instead of summing areas of bars).

• i.e., the tops of rectangles in histogram form approximately a normal curve w/same mean, variance
• how large must n be for the approximation to be good? Approximation  good if  np(1 - p) > 5.

Application
To use this result, compute probabilities for binomial random variables by finding the area under the appropriate normal curve.

ex:

In an experiment 80 trees are grown under stressful conditions. Suppose the probability of any one tree surviving is .35; what’s the probability that between 15 and 25 trees survive out of the 80?
Let X = # which survive; then X is binomial, w/ n=80, p=.35;
so
mean  m = np = 80 (.35) = 28
variance  s² = np(1 - p)  =  80(.35)(.65) = 18.2
standard deviation  s = 4.3
Want P(15 <= X <= 25).
Glitch:
• tables don’t go up to n=80
• could compute as    P(15 <= X <= 25)  =  f(15) + f(16) + ... + f(25),   using the formula for the density function, but this is time-consuming!
Approach: Use a normal distribution to approximate the probability
Let Y be a normal random variable, with mean m = 28, s.d. s = 4.3.  Then X and Y have approximately the same distribution, in the sense that if we drew the histogram corresponding to X the tops of the bars would be very closely approximated by the density function for Y.

We want
P(15 <= X <= 25)  =  area of the bars for  x = 15  to x = 25;
since the bars of the histogram are centered over their respective values, this is approximately the area under the density curve of Y  for  x  between  14.5  and  25.5  (this is called the half-unit correction):
P(15 <= X <= 25)  =  P(14.5 <= Y <= 25.5)
To compute the probability for Y, use the usual standard normal random variable technique:
Let  Z  =   
 
when  Y = 14.5,    =  -3.14

when  Y = 25.5,     =  -.58

so
P(14.5 <= Y <= 25.5)   =   P(-3.14 <= Z <= -.58)
=   P(Z <= -.58)  -  P(Z <= -3.14)
=   .2810  -  .0008   =   .2802
Thus    P(15 <= X <= 25)  =  .28,
or there's a 28% chance that between 15 and 25 trees will survive.

Flip coin 200 times; what’s probability get more than 120 heads?

Let  X = # heads that occur in 200 flips; then X is binomial, with  n = 200  and p = .5,
mean = np = 200(.5) = 100,  variance = np(1 - p)  =  200(.5)(.5)  =  50,
standard deviation  =  7.1.

Want:  P(X > 120)
Calculate using the normal approximation:  let Y be normal, with mean 100 and s.d. 7.1;
then   P(X > 120)  =  P(Y > 120.5)

Use standard normal r.v.  Z  to compute probability of normal r.v. Y:
Z = 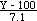;   when  Y = 120.5,  Z = 2.89,

so   P(Y > 120.5)  =  P(Z > 2.89)  =  1  -  P(Z <= 2.89)   =   1 - .9981  =  .0019.

Thus  P(X > 120)  =  .0019, i.e., there's anly about a .2% chance that we'll get more than 120 heads in 200 flips of a (fair) coin.