5.2 Expectation & Covariance
Def: Let X and Y be discrete random variables with joint
density function f(x,y), and let H(X,Y) be any function of X &
Y (or either alone). Then the expected value of H is
ex:
Consider the plant example from previous section, where X = number
of stems on a plant and Y = # of blooms. Then
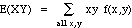
= (1)(0)f(1,0) + (1)(1)f(1,1) + (1)(2)f(1,2)
+ (2)(0)f(2,0) + (2)(1)f(2,1) + (2)(2)f(2,2)
+ (3)(0)f(3,0) + (3)(1)f(3,1) + (3)(2)f(3,2)
= (0)(.22) + (1)(.12) + (2)(0)
+ (0)(.09) + (2)(.25) + (4)(.15)
+ (0)(.01) + (3)(.07) + (6)(.09)
= 1.97
so the product of the number of stems and number of blooms averages
1.97.
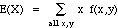
= (1)f(1,0) + (1)f(1,1) + (1)f(1,2)
+ (2)f(2,0) + (2)f(2,1) + (2)f(2,2)
+ (3)f(3,0) + (3)f(3,1) + (3)f(3,2)
= (1)(.22) + (1)(.12) + (1)(0)
+ (2)(.09) + (2)(.25) + (2)(.15)
+ (3)(.01) + (3)(.07) + (3)(.09)
= 1.83
so there are on average 1.83 stems per plant.
Could have computed E(X) using just the marginal density for X, since doesn't
involve Y: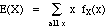
= (1) fX(1) + (2) fX(2)
+ (3) fX(3)
= (1)(.34) + (2)(.49) + (3)(.17)
= 1.83, as before
Similarly, E(Y) = .92, computed either using the joint density function
or more simply using the marginal density for Y. Thus there are on average
.92 blooms per plant.
E(X+Y) = E(X) + E(Y) from properties
of expectation
However, notice that
E(XY) <> E(X) * E(Y)
Note: denote E(X) by mX, and
E(Y) by mY.
Q: when is it the case that E(XY) = E(X) E(Y)?
Theorem: If X,Y are independent, then
Def: The covariance of X and Y is defined to be
cov(X,Y) = E((X - mX)(Y
- mY))
What does this measure?
Consider:
-
X - mX measures how far X is from
the mean for X; it's positive if X is above the mean, negative if X is
below the mean
-
Y - mY measures how far Y is from
the mean for Y; positive if Y is above the mean, negative if Y is below
the mean
-
(X - mX)(Y - mY)
-
will be positive if X and Y are both above or both below their means
-
will be negative if X is above average, Y is below, and vice-versa
-
E((X - mX)(Y - mY))
is the average value of the product
-
will be positive if above-average values of X tend to occur with
above-average values of Y
-
will be negative if above-average values of X tend to occur with below-average
values of Y
-
cov(X,Y) thus measures whether X & Y tend to "vary together"
Computational formula for covariance:
cov (X,Y) = E(XY) ? E(X)E(Y).
ex:
previous plant stuff:
cov(X,Y) = E(XY) - E(X)E(Y) = 1.97
- (1.83)(.92) = .2864
since the covariance is positive, X and Y tend to vary together: when X
is above average, Y tends to also be above average, i.e., a plant with
an above-average number of stems will also tend to have an above-average
number of blooms.
note: the magnitude of the covariance, .2864, is not directly
meaningful - just whether it's positive or negative.
Note:
-
If X & Y are independent, then cov(X,Y) = 0
-
follows because then E(XY) = E(X) E(Y)
-
makes sense: if X and Y are independent, whether X is above or below average
should have no influence on the value of Y; thus X and Y wouldn't tend
to vary together
-
Converse not true; just because cov(X,Y) = 0, doesn't mean X, Y are independent!
Previous section Next
section