5.3 Correlation Coefficient
Def: Given discrete random variables X,Y their correlation coefficient
is defined as
Gives a "normalized" value of covariance; always have
r measures the strength of the linear
relationship between X & Y. If the values of X and Y are recorded for
a lage number of experiments, and the points (X,Y) are plotted (generating
a scatter plot), then:
-
if r is near 1 or -1, points (X,Y)
will tend to fall near a line
-
the slope of the line will be positive if r
positive, negative if r negative
-
if r is near 0, the points (X,Y)
will show no clear linear trend when plotted
In fact:
-
r = 1 or -1 if and only if
X and Y are directly linearly related, Y = a + bX for some constants a,b.
-
If X,Y are independent, then r =
0 (although converse not true)
-
follows since cov(X,Y) = 0
Note: even if r = 0, X and Y may
not be independent!! May be directly related, but by a non-linear
relationship!!
ex:
plant example from previous sections:
we found before that cov(X,Y) = .2684,
E(X) = 1.83, E(Y) = .92.
need
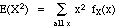
= (12) fX(1) + (22)
fX(2) + (32) fX(3)
= (12)(.34) + (22)(.49)
+ (32)(.17)
= 3.83,
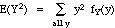
= 1.40 (in a similar fashion)
so
var(X) = E(X2) - E(X)2
= 3.83 - 1.832 = .4811
var(Y) = E(Y2) - E(Y)2
= 1.40 - .922 = .5536
Thus
The value of r is positive, about halfway between
0 and 1; thus the number of stems and number of blooms will tend to vary
together, both being above or below average, but the trend is not a particularly
strong one: it won't be the case that every plant with an above-average
number of stems will have an above-average number of blooms.
Previous section Next
section