6.1 Random Samples
Idea: have some population with unknown distribution of some
quantity ? say, heights of students in class
-
the (unknown) mean, variance, and moments of the quantity are called the
population parameters
Note: If population is finite, and you could measure values
for the whole population, could compute these parameters directly.
Suppose have m individuals in population, and their heights
are x1, x2, ..., xm.
-
finite population mean:
-
finite population variance:
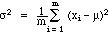
-
average squared deviation from mean!
Glitch:
-
usually, hard to get values for whole population (too hard to collect all
information)
-
if population is infinite, e.g., distribution is continuous, clearly canít
measure whole population!
Approach: choose a sample of n objects from population; use
the values for the items in the sample to estimate the values of the parameters
for whole population
-
pick at random n objects from population
-
value of interest for each depends on which object selected, i.e., is a
random variable whose distribution is that of whole populaton
-
thus have n random variables X1, X2,
..., Xn with identical (but unknown) distribution
-
assume the values of the random variables are independent, i.e., that the
value of one doesn't affect the value of another
Thus get the following definition:
Def: A random sample of size n from a particular
distribution is a set of n independent random variables X1,
X2, ..., Xn , each of which has this same distribution.
-
when we choose a particular sample, get an observed value for each of the
random variables
-
denote observed values for the sample by x1, x2,
..., xn (small x's)
-
use these values to estimate parameters for population
Previous section Next
section